(a) Acceleration of the block
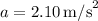
(b) Angular acceleration of the pulley
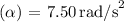
(c) Moment of inertia of the pulley

(a) Acceleration of the Block:
Using Newton's second law (F = ma), we can find the acceleration (a) of the block.
![$\[ a = \frac{7.5 \, \text{N}}{3.56 \, \text{kg}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/w92xv5pc7z8qchu6te1ay53fybryt2rvak.png)
![\[ a \approx 2.10 \, \text{m/s}^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/zjjsacroli60w9x6wbekwm5henfz7xmequ.png)
(b) Angular Acceleration of the Pulley:
![$\[ \alpha = (a)/(r) \]](https://img.qammunity.org/2024/formulas/physics/high-school/rr2wf3ubgadixfl9q846bilqsexk21bz7d.png)
![$\[ \alpha = \frac{2.10 \, \text{m/s}^2}{0.28 \, \text{m}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/h9qlqk2imb8nzg6b9b7qknyx81qes91isb.png)
![\[ \alpha \approx 7.50 \, \text{rad/s}^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/rwc8qu6c7xnmkuicomvg6a0xpdx2aim52v.png)
(c) Moment of Inertia of the Pulley:
![\[ \tau = Fr \]](https://img.qammunity.org/2024/formulas/physics/high-school/7xp7hp593hk4oeb1dxv6fc3fdyqabfhp3z.png)
![\[ \tau = (7.5 \, \text{N})(0.28 \, \text{m}) \]](https://img.qammunity.org/2024/formulas/physics/high-school/9i9t08lwfz1f3y0cs85pqymop8pziv1bws.png)
![\[ \tau \approx 2.10 \, \text{Nm} \]](https://img.qammunity.org/2024/formulas/physics/high-school/4mvbax8xhear2rq8srq1y3d70c22iiczwb.png)
Now, use the torque to find the moment of inertia:
![\[ I = (\tau)/(\alpha) \]](https://img.qammunity.org/2024/formulas/physics/college/kl39cvlv8bzaruo7lyy15g2hjjxqg1yjh2.png)
![$\[ I = \frac{2.10 \, \text{Nm}}{7.50 \, \text{rad/s}^2} \]](https://img.qammunity.org/2024/formulas/physics/high-school/ykz686zq5rbzhb3u6wllge8njxl5nfuidx.png)
![\[ I \approx 0.28 \, \text{kg} \cdot \text{m}^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/iu88iu3jo0vd4mrrwexruulhu5kagzrezc.png)
So, the calculated values are:
(a) Acceleration of the block
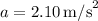
(b) Angular acceleration of the pulley
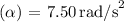
(c) Moment of inertia of the pulley
