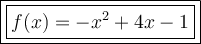Question

The table represents a quadtraric function. Write an equation in standard form.

x 1,2,3,4
f(x) 2,3,2,-1
The function is f(x) = ?
OFFERING 50 POINTS

Answer 1

`f(x)=-x^2+4x-1`

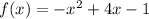
Explanation:

A quadratic function is a second-degree polynomial function of the form f(x) = ax² + bx + c.

From observation of the given table, we can see that x = 1 and x = 3 share the same y-value (y = 2). This suggests that these points are symmetric with respect to the vertex of the quadratic function, and so the x-value right in the middle of these two x-values (x = 2) corresponds to the x-coordinate of the vertex.

Therefore, the vertex of the quadratic equation is (2, 3).

`\boxed{\begin{array}{l}\underline{\sf Vertex\;form\;of\;a\;quadratic\; equation}\\\\y=a(x-h)^2+k\\\\\textsf{where:}\\\phantom{ww}\bullet\;(h,k)\;\sf is\;the\;vertex.\\\phantom{ww}\bullet\;a\;\sf is\;the\;leading\;coefficient.\\\end{array}}`

Substitute the vertex (2, 3) into the vertex form of a quadratic equation:

`y=a(x-2)^2+3`

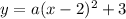
To find the value of a, substitute another point from the table into the equation. Let's use (1, 2):

`2=a(1-2)^2+3`

`2=a(-1)^2+3`

`2=a(1)+3`

`2=a+3`

`a=-1`

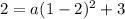
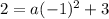
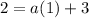
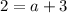
Therefore, the vertex form of the quadratic equation is:

`y=-(x-2)^2+3`

To write this in standard form y = ax² + bx + c, expand and simplify :

`y=-(x^2-4x+4)+3`

`y=-x^2+4x-4+3`

`y=-x^2+4x-1`

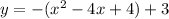
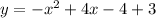
Finally, replace y with f(x):

`\large\boxed{\boxed{f(x)=-x^2+4x-1}}`