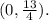The coordinates of point P are
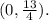
Let's denote the coordinates of point P on the y-axis as (0, y). The distance from P to the x-axis is then given by the y-coordinate (since P lies on the y-axis), and the distance from P to point F (3, 2) is given by the distance formula:
![\[ PF = √((x_2 - x_1)^2 + (y_2 - y_1)^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/q6nf1upp4zxf8lq4k5e6b855c0ml5ee8om.png)
In this case,
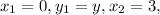 and
and
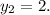 Therefore, the distance formula becomes:
Therefore, the distance formula becomes:
![\[ PF = √((3 - 0)^2 + (2 - y)^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2a5a7utaj1dzrfvecaoaxygoz1o26qw06n.png)
We want the distance from P to the x-axis to equal PF. The distance from P to the x-axis is simply the y-coordinate of P, which is y. So, we have the equation:
![\[ y = √((3 - 0)^2 + (2 - y)^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ooook52elyoat52d43ao3sdwagfm9lq3k8.png)
Solving for y:
![\[ y = √(9 + (2 - y)^2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/grjvcypqjtm7a8dgxuu90n2o4j6ndsy9lr.png)
![\[ y^2 = 9 + (2 - y)^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vrkooknvdk8hogrd0r1clb3dto4dfwbcwh.png)
![\[ y^2 = 9 + 4 - 4y + y^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/sdbx1ur0a3frx8ugwye3wgyrektx68v13l.png)
![\[ 4y = 13 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9cbk63g7flpa9q76rvypxz8gcmo29tcnzj.png)
![\[ y = (13)/(4) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yhco79rxnl4i4dtp8jm7yei1ulgolmsd5h.png)
So, the coordinates of point P are