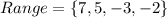Question

Determine whether the relation represents a function. If it is a function, state the domain and range. {(-3, 7), (2, 5), (5, -3), (8, -2)}

Answer 1

(a) The relation is a function

(b)

`Domain = \{-3,2,5,8\}`

`Range = \{7,5,-3,-2\}`

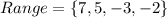
Explanation:

Given

`\{(-3, 7), (2, 5), (5, -3), (8, -2)\}`

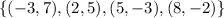
(a): Is it a function?

A relation has the form:
`\{(x_1,y_1),(x_2,y_2)....(x_n,y_n)\}`

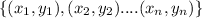
For the relation to be a function, all the x values must be unique and not repeated.

In
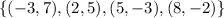`\{(-3, 7), (2, 5), (5, -3), (8, -2)\}`, the x values are: -3, 2, 5 and 8.

None of the values are repeated.

Hence, the relation is a function

(b): The domain and the range:

The x values represent the domain while the range are represented by the y values.

So, we have:

`Domain = \{-3,2,5,8\}`

`Range = \{7,5,-3,-2\}`