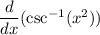Question

Solve the equation.

StartFraction d Over d x EndFraction cosecant Superscript negative 1 Baseline x squared =

StartFraction negative 2 x Over StartRoot 1 minus x Superscript 4 Baseline EndRoot EndFraction

StartFraction negative 2 Over x StartRoot x Superscript 4 Baseline minus 1 EndRoot EndFraction

StartFraction 2 Over x StartRoot x Superscript 4 Baseline minus 1 EndRoot EndFraction

StartFraction 2 x Over StartRoot 1 minus x Superscript 4 Baseline EndRoot EndFraction

Answer 1

The solution to the equation
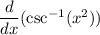`(d)/(dx)(\csc^(-1)(x^2))` is
`(dy)/(dx) = (2)/(-x\cot(\csc^(-1)(x^2))\cdot)`

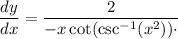
How to determine the solution to the equation

From the question, we have the following parameters that can be used in our computation:

`(d)/(dx)(\csc^(-1)(x^2))`

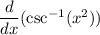
This can be expressed as

`y = \csc^(-1)(x^2)`

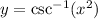
Take the cosecant of both sides

So, we have

`\csc(y) = x^2`

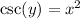
Next, we differentiate both sides

`-\cot(y)\csc(y) (dy)/(dx) = 2x`

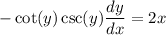
Make dy/dx the subject

`(dy)/(dx) = (2x)/(-\cot(y)\csc(y) )`

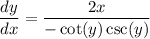
Recall that
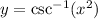`y = \csc^(-1)(x^2)` and
`\csc(y) = x^2`

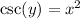
So, we have

`(dy)/(dx) = (2x)/(-\cot(\csc^(-1)(x^2))\cdot x^2 )`

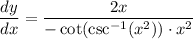
Divide

`(dy)/(dx) = (2)/(-x\cot(\csc^(-1)(x^2))\cdot)`

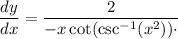
Hence, the solution to the equation is
`(dy)/(dx) = (2)/(-x\cot(\csc^(-1)(x^2))\cdot)`

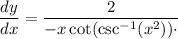
Question

Solve the equation
`(d)/(dx)(\csc^(-1)(x^2))`