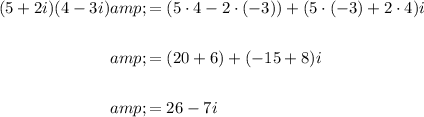Answer:
![\textsf{1)}\quad 2x^2y^3 z^4\:\sqrt[4]{8xz}](https://img.qammunity.org/2024/formulas/mathematics/college/6k4y392g0c2toc87yn1bz655s44o0achkp.png)
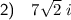
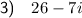
Explanation:
Question 1
Given expression:
![\sqrt[4]{128x^9y^(12)z^(17)}](https://img.qammunity.org/2024/formulas/mathematics/college/7x4tjno7x10n8ms8ycuws0mcgzrm57t0e7.png)
First, rewrite 128 as a product of its prime factors: 128 = 2⁷
![\sqrt[4]{2^7x^9y^(12)z^(17)}](https://img.qammunity.org/2024/formulas/mathematics/college/gysyau7emcz88iano2eia31wnxd9qf85nu.png)

![\sqrt[4]{2^7}\;\sqrt[4]{x^9}\;\sqrt[4]{y^(12)}\;\sqrt[4]{z^(17)}](https://img.qammunity.org/2024/formulas/mathematics/college/h1tn2ofncds5me9974c7ygrysombeaf70n.png)
Rewrite the exponents of each term so that the sums of the exponents include multiples of 4:
![\sqrt[4]{2^(4+3)}\;\sqrt[4]{x^(8+1)}\;\sqrt[4]{y^(12)}\;\sqrt[4]{z^(16+1)}](https://img.qammunity.org/2024/formulas/mathematics/college/j1s6u2h6iu1ky9dqz7kvv798ihtsqvifa5.png)
Apply the product exponent rule:
![\sqrt[4]{2^(4)\cdot 2^(3)}\;\sqrt[4]{x^8\cdot x}\;\sqrt[4]{y^(12)}\;\sqrt[4]{z^(16)\cdot z}](https://img.qammunity.org/2024/formulas/mathematics/college/95y6sakobfwp0rv48roi6t8yfnhw1ooq7u.png)
Apply the power of a product exponent rule to x⁸, y¹² and z¹⁶ so that their outer exponents are 4:
![\sqrt[4]{2^(4)\cdot 2^(3)}\;\sqrt[4]{(x^2)^4\cdot x}\;\sqrt[4]{(y^3)^4}\;\sqrt[4]{(z^4)^4\cdot z}](https://img.qammunity.org/2024/formulas/mathematics/college/x4nycbjf6k3xoajolh6stpubtaz2qajm2d.png)

![\sqrt[4]{2^(4)}\;\sqrt[4]{2^(3)}\;\sqrt[4]{(x^2)^4}\;\sqrt[4]{x}\;\sqrt[4]{(y^3)^4}\;\sqrt[4]{(z^4)^4}\;\sqrt[4]{z}](https://img.qammunity.org/2024/formulas/mathematics/college/43c9vcw1w4sntjeldf7in3qyl4jcsr6n66.png)
![\textsf{Apply the exponent rule:} \quad \sqrt[n]{a^n}=a](https://img.qammunity.org/2024/formulas/mathematics/college/hifipq8myudlkro1shb1942d6y0tot1wmv.png)
![2 \cdot \sqrt[4]{2^(3)}\cdot x^2 \cdot\sqrt[4]{x}\cdot y^3\cdot z^4\cdot\sqrt[4]{z}](https://img.qammunity.org/2024/formulas/mathematics/college/hg4819c9kemyn3q0xksigp6ti2rkaobd2i.png)
![2 \cdot \sqrt[4]{8}\cdot x^2 \cdot\sqrt[4]{x}\cdot y^3\cdot z^4\cdot\sqrt[4]{z}](https://img.qammunity.org/2024/formulas/mathematics/college/ljmglf7fx8i95vg0v5joja6uikeyrhny73.png)
Rearrange to collect like terms:
![2x^2y^3 z^4\;\sqrt[4]{8}\;\sqrt[4]{x}\;\sqrt[4]{z}](https://img.qammunity.org/2024/formulas/mathematics/college/kik26irdcastkhh99kipu4wcmbybgubdr9.png)

![2x^2y^3 z^4\;\sqrt[4]{8xz}](https://img.qammunity.org/2024/formulas/mathematics/college/9m94mb4we211werzypekhdp9na0u03kcl9.png)

Question 2
Given expression:
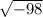
First, rewrite 98 as 98 × (-1):
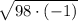
Rewrite 98 as a product of its prime factors: 98 = 7² × 2
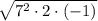

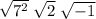
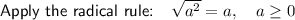
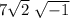

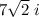

Question 3
Given expression:
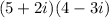
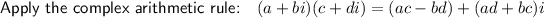
In this case:
Therefore: