Question

PLEASE PLEASE PLEASE HELP THIS ENDS IN LESS THAN A DAY I NEED YOUR HELP BADLY LOOK AT THE PICTURE BELOW

Answer 1

`\textsf{1)}\quad 5(x - 4)(x - 5)`

`\textsf{2)}\quad (2x + 1)(6x - 5)`

`\textsf{3)}\quad (8x^3 + 5)(64x^6 - 40x^3 + 25)`

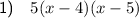
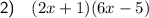
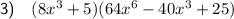
Explanation:

Factoring is the method of finding the numbers or expressions that multiply together to give a specific mathematical expression.

`\hrulefill`

Question 1

To factor the quadratic expression 5x² - 45x + 100, we can use the method of factoring by grouping.

Split the middle term (-45x) into two terms whose coefficients multiply to the product of the leading coefficient (5) and the constant term (100) and whose sum is -45. Group the terms in pairs, then factor.

`\begin{aligned}5x^2-45x+100&=5x^2-25x-20x+100\\&=[5x^2-25x]-[20x-100]\\&=5x(x-5)-20(x-5)\\&=(5x-20)(x-5)\\&=5(x-4)(x-5)\end{aligned}`

`\hrulefill`

Question 2

To factor the quadratic expression 12x² - 4x - 5, we can use the method of factoring by grouping.

Split the middle term (-4x) into two terms whose coefficients multiply to the product of the leading coefficient (12) and the constant term (-5) and whose sum is -4. Group the terms in pairs, then factor.

`\begin{aligned}12x^2-4x-5&=12x^2+6x-10x-5\\&=[12x^2+6x]-[10x+5]\\&=6x(2x+1)-5(2x+1)\\&=(2x+1)(6x-5)\end{aligned}`

`\hrulefill`

Question 3

To factor 512x⁹ + 125, begin by rewriting both terms as cubes.

512 is the cube of 8, and 125 is the cube of 5:

`\begin{aligned}512x^9 + 125&=8^3 \cdot x^9+5^3\\&=8^3 \cdot (x^3)^3 + 5^3\\&=(8x^3)^3+5^3\end{aligned}`

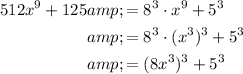
Now we can apply the sum of cubes formula:

`\boxed{a^3+b^3=(a+b)(a^2-ab+b^2)}`

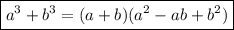
In this case a = 8x³ and b = 5:

`\begin{aligned}512x^9 + 125&=(8x^3)^3+5^3\\&=(8x^3+5)((8x^3)^2-8x^3\cdot 5+5^2)\\&=(8x^3+5)(64x^6-40x^3+25)\\\end{aligned}`