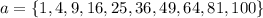Answer:
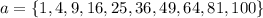
Explanation:
Given
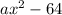
Required
Determine possible values of a
For the expression to be a difference of two squares, then a must be a perfect square between 1 and 100 (inclusive).
Let
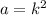 where
where
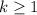
When k = 1
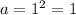
k = 2
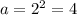
k=3
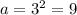
It goes on until k = 10
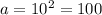
So, the possible values of a are: