Answer:
The perimeter of triangle ΔABC is approximately;
(A) 20.0
Explanation:
In ΔABC, the coordinates of the vertices are given as follows;
A(-4, 1), B(-2, 3), C(3, -4)
The length, 'l', of the sides of the triangle with known 'x', am]nd 'y' coordinates are given as follows;
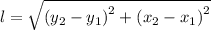
Therefore, we have;
The length of segment
 = √((3 - 1)² + (-2 - (-4))²) = 2·√2 ≈ 2.83
= √((3 - 1)² + (-2 - (-4))²) = 2·√2 ≈ 2.83
The length of segment
 = √(((-4) - 3)² + (3 - (-2))²) = √74 ≈ 8.6
= √(((-4) - 3)² + (3 - (-2))²) = √74 ≈ 8.6
The length of segment
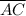 = √(((-4) - 1)² + (3 - (-4))²) = √74 ≈ 8.6
= √(((-4) - 1)² + (3 - (-4))²) = √74 ≈ 8.6
The perimeter of a geometric shape is equal to the sum of the length of sides of the figure
The perimeter of triangle ΔABC = (The length of segment
 ) + (The length of segment
) + (The length of segment
 ) + (The length of segment
) + (The length of segment
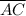 )
)
∴ The perimeter of triangle ΔABC = 2·√2 + √74 + √74 ≈ 20.0.