Answer:
C
Explanation:
We want the equation of the line that passes through (3, 6) and is perpendicular to:
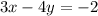
First, convert the second equation into slope-intercept form:
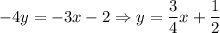
So, we can see that the slope of the line is 3/4.
The slopes of perpendicular lines are negative reciprocals of each other.
Therefore, the slope of the new line is -4/3.
It passes through the point (3, 6).
We can use the point-slope form:
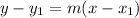
Substitute:
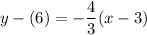
Distribute:
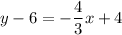
Therefore:

The answer is C.