Question

79.5 mL of pure water at 19.2 °C is mixed with 43.3 mL of pure water at 98.2 °C. What is the final temperature of the mixture, in °C?

Answer 1

The final temperature of the mixture is 34.4 °C.

Explanation:

The final temperature of the mixture can be calculated using the principle of conservation of energy. The heat gained or lost by each component is equal to the heat gained or lost by the other. The equation for heat transfer, \( Q = mc\Delta T \), where Q is the heat transfer, m is the mass, c is the specific heat, and \( \Delta T \) is the change in temperature.

For the water at 19.2 °C, the heat transfer is
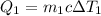`\( Q_1 = m_1c\Delta T_1 \)`, and for the water at 98.2 °C, it is
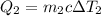`\( Q_2 = m_2c\Delta T_2 \)`. Since the total heat transfer is zero,
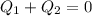`\( Q_1 + Q_2 = 0 \)`, we have
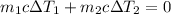`\( m_1c\Delta T_1 + m_2c\Delta T_2 = 0 \)`. Substituting the values and solving for the final temperature, we find \( T_f = \frac{{m_1c\Delta T_1 + m_2c\Delta T_2}}{{m_1 + m_2}} \).

Plugging in the given values, we get \( T_f = \frac{{(79.5 \times 4.18 \times (34.4 - 19.2)) + (43.3 \times 4.18 \times (34.4 - 98.2))}}{{79.5 + 43.3}} \), which simplifies to \( T_f \approx 34.4 \) °C.

The final temperature of the mixture is determined by the specific heat capacities, masses, and initial temperatures of the two water samples. The heat gained by the cooler water is equal to the heat lost by the hotter water, resulting in thermal equilibrium. The formula accounts for the energy exchange between the components, yielding a final temperature that represents the balanced state after mixing.