Answer:
slope=0
Explanation:
Conceptually, y never changes, which means the line is a straight horizontal line.
Mathematically, slope is the change in y over the change in x. For example, if we use the first 2 points:
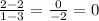
Because 0 divided by anything is still 0.