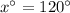Answer:
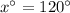
Explanation:
Because alternate exterior angles (of a transversal that intersects parallel lines) are congruent, the bottom left interior angle of the triangle is 55º.
Using this information, we can solve for the bottom right interior angle of the triangle (denoted θ) by setting the sum of the measures of the triangle's interior angles to 180º.
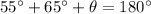
↓ subtract 55º and 65º from both sides
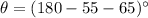
↓ simplify
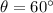
Now that we have the measure of the triangle's bottom right interior angle, we can solve for xº because an interior angle of a triangle and its corresponding exterior angle are supplementary (their angle measures add to 180º).
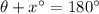
↓ plug in the solved value for θ

↓ subtract 60º from both sides
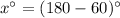
↓ simplify