Question

Function A and Function B are linear functions.

(See photo attached)
Select all the statements that are true.
1. The slope of Function A is less than the slope of Function B.
2. The slope of Function A is equal to the slope of Function B.
3. The y-value of Function A when x=2 is less than the y-value of function B when x=2
4. The y-value of function A when x=2 is greater than the y-value of function b when x=2

Answer 1

The statement that is true is the fourth statement

4. The y-value of function A when x = 2 is greater than the y-value of function b when x = 2

The steps to obtain the true statement can be presented as follows;

The slope of a function with known ordered pairs, (x₁, y₁), and (x₂, y₂), can be found using the formula;

`Slope=(y_2-y_1)/(x_2-x_1)`

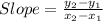
The slope of the function B using the ordered pair (-4, -4), and (6, 11) therefore is; (11 - (-4))/(6 - (-4)) = 3/2

The slope of the function B = 3/2

Therefore, the slope of function A is greater than the slope of function B

The equation of the function B is therefore;

y - (-4) = (3/2)·(x - (-4))
y + 4 = (3/2) × (x + 4)

y = 3·x/2 + 6 - 4

y = 3·x/2 + 2

When x = 2, we get;

The value of the function A is; y = (5/2) × 2 + 3

(5/2) × 2 + 3 = 8

y = 8

The value of the function B is; y = (3/2) × 2 + 2

(3/2) × 2 + 2 = 5

y = 5

The y-value of function A when x = 2 is greater than the y-value of function b when x = 2