The linear regression line equation for the birth rate percent for a specified number of years since 1985, obtained using the least squares method is; y = 9.4321 + 0.8564·x
The steps used to find the linear regression line equation can be presented as follows;
Let x represent the number of years since 1985 and let x represent the birth rate percent. The least squares regression line equation can be presented as follows;
y = a + b·x
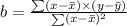
The table of values indicates that we get;
 = 15
= 15
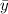 = 22.27857
= 22.27857
 = 599.5
= 599.5
 = 700
= 700
b = 599.5/700
599.5/700 ≈ 0.8564
b ≈ 0.8564
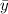 = a + b·
= a + b·

a =
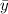 - b·
- b·

a = 22.27857 - (599.5/700) × 15
22.27857 - (599.5/700) × 15 ≈ 9.4321
The linear regression line equation is; y = 9.4321 + 0.8564·x