The exact values of sin
 , csc
, csc
 , and cot
, and cot
 are:
are:
sin
 =
=
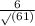
csc
 =
=
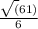
cot
 = -5 / 6
= -5 / 6
How to find the exact values
To find the exact values of sin
 , csc
, csc
 , and cot
, and cot
 , determine the values of the trigonometric ratios based on the given point (-5, 6) on the terminal side of
, determine the values of the trigonometric ratios based on the given point (-5, 6) on the terminal side of
 .
.
Using the given coordinates, calculate the radius (r) and the angle (
 ) using the formulas:
) using the formulas:
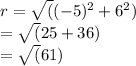
 = arctan(y/x) = arctan(6/(-5))
= arctan(y/x) = arctan(6/(-5))
Let's calculate the values:
sin
 = y / r =
= y / r =
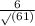
csc
 = 1 / sin
= 1 / sin
 =
=
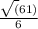
cot
 = x / y = -5 / 6
= x / y = -5 / 6
Therefore, the exact values of sin
 , csc
, csc
 , and cot
, and cot
 are:
are:
sin
 =
=
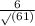
csc
 =
=
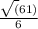
cot
 = -5 / 6
= -5 / 6