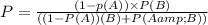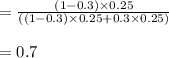Question

Problem: A federal agency is deciding which of two waste dump projects to investigate. A top administrator estimates that the probability of federal law violations is 0.30 at the first project and 0.25 at the second project. Also, he believes the occurrences of violations in these two projects are mutually exclusive (that is, the events are disjoint).

a). find the probability of federal law violations in the first project or the second project.
b). given that there is not a federal law violation in the first project, find the probability that there is a federal law violation in the second project.
c). In reality, the administrator confused mutually exclusive and independent, and the events are actually independent. Answer (a) and (b) with this correct information.

Answer 1

Following are the solution to the given points:

Explanation:

For point (a) :

In this, two points are exclusive to one another, it is a probability that first or the second project will have breaches,

`\to P = P(A) + P(B)`

`= 0.3 + 0.25\\\\= 0.55`

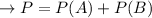
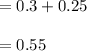
Since the p(A & B)=0 is mutually exclusive.

For point (b):

`\to P = ( (1 -p(A)) * P(B))/(((1-P(A)) * P(B) + P(A&B))) \\\\`

`= ((1 -0.3)* 0.25)/((1-0.3)*0.25 + 0) \\\\ = 1`

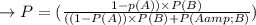
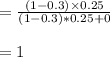
For point (c):

if both a and b are independent:

(a):

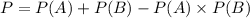
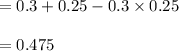
`P = P(A) + P(B) - P(A)* P(B) \\\\`

`= 0.3 + 0.25 - 0.3 * 0.25\\\\ = 0.475`

(b):

`P = ((1 -p(A)) * P(B))/(((1-P(A)) *P(B) + P(A&B))) \\\\`

`= ((1 - 0.3)* 0.25)/(((1-0.3)*0.25 + 0.3*0.25))\\\\ = 0.7`