Solution :
A). As the time passes the temperature of the coffee tends to acquire the temperature of the room, so the limiting value of the temperature of the coffee is 20°C. i.e.
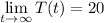
B). And limiting value of rate of cooling is given by :
![$\lim_(t \to \infty) \ (dT)/(dt) =\lim_(t \to \infty) \ [k(T-T_(room))] $](https://img.qammunity.org/2022/formulas/mathematics/college/g5gkcdg7xazi34rpz4xjvwmmvf0dezdo9q.png)
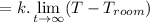
![$=k .[ \lim_(t \to \infty) T-\lim_(t \to \infty) T_(room)]$](https://img.qammunity.org/2022/formulas/mathematics/college/c5qrbigqn8nocxkpy4supzt36ez5socbf7.png)
![$=k.[T_(room)-T_(room)]$](https://img.qammunity.org/2022/formulas/mathematics/college/kvpb5tlzpp7x3cn8wl61vncl9bqm3skga8.png)
= k. 0
= 0
C). Given,
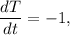 when T(t) = 70° using this in the given equation,
when T(t) = 70° using this in the given equation,
-1 = k.(70-20)
k = -0.02
D). By Euler method, we get
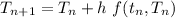
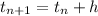
where,
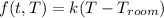
= -0.02(T - 20)
We have
 at t = 0 and h = 2.
at t = 0 and h = 2.
So
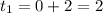
∴
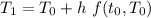
= 90+2[-0.02(90-20)]
= 87.2
At
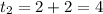
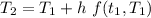
= 87.2+2[-0.02(87.2-20)]
= 84.51
At
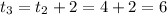

= 84.51+2[-0.02(84.51-20)]
= 81.93
At
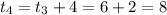
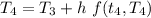
= 81.93+2[-0.02(81.93-20)]
= 79.45
At
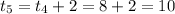
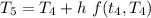
= 79.45+2[-0.02(79.45-20)]
= 77.07
So after 10 minutes, the temperature of the coffee will be 77.07°C.