Question

An astronaut named Sandra Bullock has drifted too far away from her spaceshuttle while attempting to repair the Hubble Space telescope. She realizes that theshuttle is moving away from her at 3 m/s. On her back is a 10 kg jetpack which consistsof an 8 kg holding tank filled with 2 kg of pressurized gas. Without the jetpack, sheand her space suit have a mass of 80 kg.

Required:
a. She is able to use the gas to propel herself in the same direction as the shuttle. The gas exits the tank at a uniform rate with a constant velocity of 100 m/s, relative to the tank (and her). After the gas in the tank has been released, what is her velocity?
b. After this, she throws her empty tank into space and relies on the conservation of momentum to increase her speed to match that of the shuttle. With what velocity (in her frame of reference!) will she have to throw the tank?

Answer 1

a) v_f = 0.898 m / s, b) v₂ = -6.286 m / s

Step-by-step explanation:

a) For this exercise we use the conservation of momentum, we define a system formed by the astronaut, her equipment and the expelled gases. We must also define a stationary frame of reference, let's place the system on the platform, so the speed of the subject is v = -3 m / s

Initial instant. Before you start to pass gas

p₀ = (M + Δm) v

M is the mass of the astronaut M = 80Kg and Δm the masses of the gases

Final moment. When you expel the gases

p_f = M (v + Δv) + Δm (v-v_e)

where v_e is the gas velocity v_e = 100 m / s

momentum is conserved

p₀ = p_f

M v + Δm v = Mv + M Δv + Δm v -Δm ve

0 = M Δv - Δm v_e

if we make the very small quantities Δv → dv and Δm → dm, furthermore the quantity of output gas is equal to the decrease in the total mass dm = -dM

M dv = -v_e dM

∫ dv = - v_e ∫ dM / M

We solve, between the lower limits v₀ = v with M = M₀ and the upper limit v = v_f for M = M_f

v_f - v₀ = - v_e (ln M_f - Ln M₀)

v_f - v₀ = v_e ln (
`(M_o)/(M_f)`)

v_f = v₀ + v_e ln (\frac{M_o}{M_f})

let's calculate

v_f = -1.3 + 100 ln (80 + 10 + 2/80 + 10)

v_f = -1.3 +2.20

v_f = 0.898 m / s

b) launch the jetpack to increase its speed up to the speed of the platform

initial instant. Before launching the tanks

p₀ = (M + m') v_f

final instnte. After launching the tanks

p_f = M v₁ + m' v₂

indicate that the final velocity of the astronaut is the platform velocity v₁=0 m / s, since the reference system is fixed on it

p₀ = p_f

(M+ m) v_f = M v₁ + m v₂2

v₂ =
`( M ( v_f - v_o) + m' v_f)/(m')`

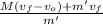
v₂ =
`(M)/(m)` (v_f -v₁) + v_f

let's calculate

v₂ = 80/10 (0.898 - 0) + 0.898

v₂ = -7.1874 + 0.898

v₂ = -6.286 m / s