Answer:
Explanation:
The missing equation is:
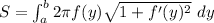
Suppose f = nonnegative function whose first derivative is within (a,b) and it is continuous, Then the area of the surface generated is revolved about the x-axis:
The area of the surface revolution is:
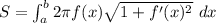
So; if
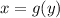 for
for
![y \ \varepsilon \ [c,d]](https://img.qammunity.org/2022/formulas/mathematics/college/ytvy09z7obzcmzhbuj9mpqmqjqgafdtbk2.png)
Then; substituting a with c and b with d; f(x) also with g(y) and dx with dy;
Then;
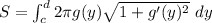
SInce;
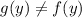 ; Then the statement is false.
; Then the statement is false.
Provided that the semicircle
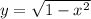 isn't on
isn't on
![[-1,1]](https://img.qammunity.org/2022/formulas/mathematics/college/t9m8dmoy91ynjrjk45zueg62lelrkdv8pe.png) interval.
interval.
Then, the solid generated by the revolution about the x-axis is a sphere.
However, the surface is well defined and the statement is false.