Answer:
(a)
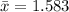 -- Population Mean
-- Population Mean
(b)
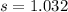 --- Population standard deviation
--- Population standard deviation
(c) See Explanation
Explanation:
Given:
Cigarette tax for 20 regions
Solving (a): The population mean
This is calculated as:
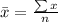
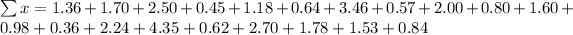
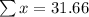

So, we have:
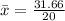
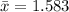
Solving (b): The population standard deviation
This is calculated as:
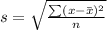


So:
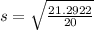
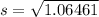
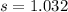
Solving (c):
Population mean tells the average amount while the standard deviation represents the spread from the calculated mean
Option (4) is correct