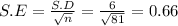Question

The average age at which adolescent girls reach their adult height is 16 years. Suppose you have a sample of 27 adolescent girls who are developmentally delayed, and who have an average age at which they reached their adult height of 17.1 years and a sample variance of 36.0 years. You want to test the hypothesis that adolescent girls who are developmentally delayed have a different age at which they reached their adult height than all adolescent girls.

Calculate the t statistic. To do this, you first need to calculate the estimated standard error. The estimated standard error is SM=_________ .The t statistic is _________. Now suppose you have a larger sample size n 81. Calculate the estimated standard error and the t statistic for this sample with the same sample average and the same standard deviation as above, but with the larger sample size. The new estimated standard error is __________ .The new t statistic is___________

Answer 1

a) t-statistic t = 0.9532

b) The standard error S.E = 1.2

c) The new t-statistic = 1.95

d) The new estimated standard error =0.666

Explanation:

Step(i):-

Given that the mean of the Population = 16

The sample size n=27

The mean of the sample = 17.1

Given that the variance of the sample (S²) = 36.0

The standard deviation of the sample (S) = √36 = 6

Test statistic

`t = (x^(-) -mean)/((S.D)/(√(n) ) )`

`t = (17.1 -16)/((6)/(√(27) ) )`

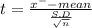
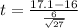
t = 0.9532

b)

The standard error is defined by

`S.E = (S.D)/(√(n) ) = (6)/(√(27) ) =1.154`

Step(ii):-

c) given that the sample size n = 81

Test statistic

`t = (x^(-) -mean)/((S.D)/(√(n) ) )`

`t = (17.1 -16)/((6)/(√(81) ) )`

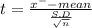
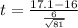
t = 1.65

d)

The new standard error is defined by

`S.E = (S.D)/(√(n) ) = (6)/(√(81) ) = 0.66`