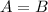Question

The Students' Conjectures Emily and Zach have two different polynomials to multiply: Polynomial product A: (4x2 – 4x)(x2 – 4) Polynomial product B: (x2 + x – 2)(4x2 – 8x)

Answer 1

Complete Question:

Emily and Zach have two different polynomials to multiply: Polynomial product A: (4x2 – 4x)(x2 – 4) Polynomial product B: (x2 + x – 2)(4x2 – 8x) They are trying to determine if the products of the two polynomials are the same. But they disagree about how to solve this problem.

Answer:

`A = B`

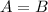
Explanation:

See comment for complete question

Given

`A: (4x^2 - 4x)(x^2 - 4)`

`B: (x^2 + x - 2)(4x^2 - 8x)`

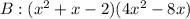
Required

Determine how they can show if the products are the same or not

To do this, we simply factorize each polynomial

For, Polynomial A: We have:

`A: (4x^2 - 4x)(x^2 - 4)`

Factor out 4x

`A: 4x(x - 1)(x^2 - 4)`

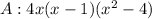
Apply difference of two squares on x^2 - 4

`A: 4x(x - 1)(x - 2)(x+2)`

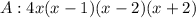
For, Polynomial B: We have:

`B: (x^2 + x - 2)(4x^2 - 8x)`

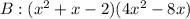
Expand x^2 + x - 2

`B:(x^2 + 2x - x - 2)(4x^2- 8x)`

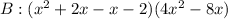
Factorize:

`B:(x(x + 2) -1(x + 2))(4x^2- 8x)`

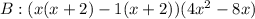
Factor out x + 2

`B:(x -1) (x + 2)(4x^2- 8x)`

Factor out 4x

`B:(x -1) (x + 2)4x(x- 2)`

Rearrange

`B: 4x(x - 1)(x - 2)(x+2)`

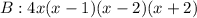
The simplified expressions are:

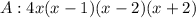`A: 4x(x - 1)(x - 2)(x+2)` and

`B: 4x(x - 1)(x - 2)(x+2)`

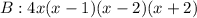
Hence, both polynomials are equal

`A = B`