Answer:
Following are the solution to the given question:
Explanation:
Please find the complete question in the attached file.
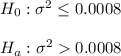
The testing states value is:
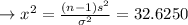
therefor the
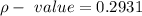
Through out the above equation its values Doesn't rejects the H_0 value, and its sample value doesn't support the claim that although the configuration of its dependent variable has been infringed.