Question

Suppose 65% of jurors come to a just decision. In a jury of ten people, what is the probability more than half come to a just decision? 0.7515 0.2485 0.0949 0.8374 0.9051

Answer 1

Answer: 0.7515

Explanation:

Binomial probability formula:

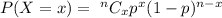`P(X=x)=\ ^nC_xp^x(1-p)^(n-x)` , where

n = total number of trials.

p= probability of success in each trial.

x= Number of successes.

Let x be a binomial variable that represents the number of jurors come to just decision.

p= 0.65

n= 10

Required probability=
`P(x>5)=P(x=6)+P(x=7)+P(x=8)+P(x=9)+P(x=10)\\\\ =\ ^(10)C_6(0.65)^6(0.35)^4+ ^(10)C_7(0.65)^7(0.35)^3+ ^(10)C_8(0.65)^8(0.35)^2+ ^(10)C_9(0.65)^9(0.35)^1+^(10)C_(10)(0.65)^(10)(0.35)^0\\\\=0.75149550912\approx0.7515`

Hence, the probability more than half come to a just decision = 0.7515