Question

Fill in the missing values below one at a time to find the quotient when 4, x, cubed, plus, 8, x, squared, plus, x, minus, 34x 3 +8x 2 +x−3 is divided by x, plus, 1x+1.

Answer 1

The division of the polynomial 4x³ + 8x² +x - 3 by x + 1 using the long polynomial division method is 4x² + 4x - 3. See image below for visual explanation.

Division of polynomial using long division.

Long division polynomial is a long process of using a polynomial know as divisor to divide another polynomial called the dividend.

In this question we are to divide:
`(4x^3+8x^2+x-3)/(x+1)`. To start, we divide the first term of the dividend(4x³) by the first term of the divisor(x) i.e.

`(4x^3)/(x)=4x^2`.

We write down the calculated result 4x² in the upper part of the table, then multiply it by the divisor 4x² ×(x × 1) = 4x³ + 4x²

Subtract this result from the dividend :

= (4x³ + 8x² + x - 3) - (4x³ + 4x²)

= 4x² + x - 3

Divide the first term of the dividend by the first term of the divisor
`(4x^2)/(x)=4x`, we now write this result to the upper part of the table, Multiply it by the divisor 4x(x + 1) = 4x² + 4x

subtract it from the remainder.

(4x² + x - 3) - (4x² + 4x) = -3x - 3

Divide the first term of the dividend by the first term of the divisor:
`(-3x)/(x)=-3`

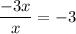
Write the result (-3) in the upper part of the table. Multiply the divisor -3(x+1) = -3x - 3

Subtract the result from the remainder.

(-3x - 3) - (-3x - 3) = 0