Question

3. İki sayıdan biri diğerinden 4 fazladır. Büyük

sayının 2 katı ile küçük sayının 5 katının
toplamı 120'dir. Buna göre büyük sayı kaçtır?
K 20
E 16
M 22


ACİL ÇÖZÜN LÜTFEN BOŞ CEVAPLARI ŞİKAYET EDİCEM​

Answer 1

E

Explanation:

50 × 2 =100 cevap 120 olucak ve 4 fazla o zaman 120 +4 =124 ediyor yani 16 daha eklememiz lazım cevap E

Answer 2

The larger number is 20.

Let's denote the larger number as x and the smaller number as y .

According to the given information, one number is 4 more than the other, which can be expressed as the equation: x = y + 4

The sum of twice the larger number and five times the smaller number is 120:
`\[ 2x + 5y = 120 \]`

Now, substitute the expression for x from the first equation into the second equation:

`\[ 2(y + 4) + 5y = 120 \]`

Distribute and combine like terms:

`\[ 2y + 8 + 5y = 120 \]`

`\[ 7y + 8 = 120 \]`

Subtract 8 from both sides:

`\[ 7y = 112 \]`

Divide by 7:

y=16

Now, substitute the value of y back into the equation for x:

`\[ x = y + 4 = 16 + 4 = 20 \]`

So, the correct solution is
`\( x = 20 \)` and
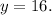`\( y = 16 \).` The larger number is 20.