Question

Find the volume of the solid obtained by rotating the region bounded by y=4x and y=2sqrt(x) about the line x=6.

Answer 1

Check the picture below.

so by graphing those two, we get that little section in gray as you see there, now, x = 6 is a vertical line, so we'll have to put the equations in y-terms and this is a washer, so we'll use the washer method.

`y=4x\implies \cfrac{y}{4}=x\qquad \qquad y=2√(x)\implies \cfrac{y^2}{4}=x~\hfill \begin{cases} \cfrac{y}{4}=x\\\\ \cfrac{y^2}{4}=x \end{cases}`

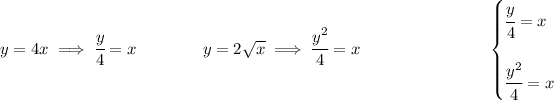
the way I get the radii is by using the "area under the curve" way, namely, I use it to get R² once and again to get r² and using each time the axis of rotation as one of my functions, in this case the axis of rotation will be f(x), and to get R² will use the "farthest from the axis of rotation" radius, and for r² the "closest to the axis of rotation".

`\stackrel{R}{\stackrel{f(x)}{6}-\stackrel{g(x)}{\cfrac{y^2}{4}}}\qquad \qquad \stackrel{r}{\stackrel{f(x)}{6}-\stackrel{g(x)}{\cfrac{y}{4}}}~\hfill \stackrel{R^2}{\left( 6-\cfrac{y^2}{4} \right)^2}-\stackrel{r^2}{\left( 6-\cfrac{y}{4} \right)^2} \\\\\\ \stackrel{\textit{doing a binomial expansion and simplification}}{3y-3y^2-\cfrac{y^2}{16}+\cfrac{y^4}{16}}`

now, both lines if do an equation on where they meet or where one equals the other, we'd get the values for y = 0 and y = 1, not surprisingly in the picture.

`\displaystyle\pi \int_0^1\left( 3y-3y^2-\cfrac{y^2}{16}+\cfrac{y^4}{16} \right)dy\implies \pi \left( \left. \cfrac{3y^2}{2} \right]_0^1-\left. y^3\cfrac{}{} \right]_0^1-\left. \cfrac{y^3}{48}\right]_0^1+\left. \cfrac{y^5}{80} \right]_0^1 \right) \\\\[-0.35em] ~\dotfill\\\\ ~\hfill \cfrac{59\pi }{120}~\hfill`