Question

AB, BC and CD are three sides of a regular polygon with centre o.

ABX is a straight line.
Angle BCD = 140°
0 Calculate the size of each of the angles marked v, w, x, y and z.


Pls help 10 points

Answer 1

Explanation:

Since, BC and DC are the sides of a regular polygon,

m(DC) = m(BC)

Opposite angles of these equal sides will be equal in measure.

m∠DBC = m∠CDB = v

By triangle sum theorem,

m∠DBC + m∠CDB + m∠DCB = 180°

v + v + 140° = 180°

2v = 40°

v = 20°

Since angle 'x' is an exterior angles of ΔBCD,

x = m∠BDC + m∠CBD [By the property of exterior angles]

x = v + v

x = 40°

Since, angles v, w and x are the linear angles,

v + w + x = 180°

20° + w + 40° = 180°

w = 120°

Since, measure of exterior angle =
`(360)/(n)`

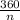
n = Number of sides

40° =
`(360)/(n)`

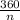
n = 9

Sum of angles formed at the center by joining vertices of the polygon = 360°

Measure of each angle at the center of a polygon with 9 sides =
`(360)/(9)`

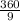
= 40°

Since, z = 3 × (Measure of central angle formed at the center)

= 3 × 40°

= 120°

In ΔOAB,

m∠OAB + m∠OBA + m∠AOB = 180°

y + y + 40° = 180° [m∠OAB = m∠OBA, Opposite angles of the equal sides OA and OB]

2y = 140°

y = 70°