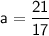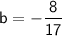Answer:
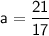
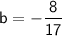
Explanation:
To find the values of
 and
and
 such that the given expression becomes an identity, we can use partial fraction decomposition. The expression in question is:
such that the given expression becomes an identity, we can use partial fraction decomposition. The expression in question is:
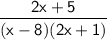
The denominator can be factored as:
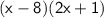 .
.
Now, we express the given fraction as the sum of two fractions with unknown values
 and
and
 :
:
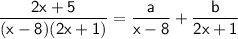
To find
 and
and
 , we can clear the denominators by multiplying both sides of the equation by the common denominator
, we can clear the denominators by multiplying both sides of the equation by the common denominator
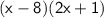 . This gives:
. This gives:
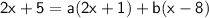
Now, we can solve for
 and
and
 by comparing coefficients. Let's expand the right side:
by comparing coefficients. Let's expand the right side:
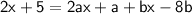
Now, group like terms:
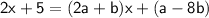
By comparing coefficients, we can write a system of equations:
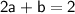
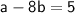
Solving this system will give us the values of
 and
and
 that turn the equation into an identity. Let's solve the system:
that turn the equation into an identity. Let's solve the system:
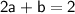
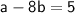
Multiplying the second equation by 2 to match coefficients:
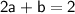
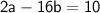
Subtracting the first equation from the second:


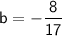
Now, substitute the value of
 back into one of the original equations. Using the first equation:
back into one of the original equations. Using the first equation:
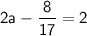
Multiply both sides by 17 to get rid of the fraction:
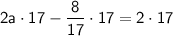
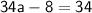
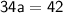
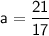
So, the values of
 and
and
 that turn the given expression into an identity are:
that turn the given expression into an identity are: