Answer:
 .
.
Step-by-step explanation:
Let
 denote the displacement of the ball. It is given that
denote the displacement of the ball. It is given that
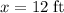 . Apply unit conversion and ensure that the displacement
. Apply unit conversion and ensure that the displacement
 of the ball is measured in meters:
of the ball is measured in meters:
 .
.
Let
 denote the initial velocity of the ball, and let
denote the initial velocity of the ball, and let
 denote the velocity of the ball right before it hits the ground. Note that since the question states the ball was "dropped", assume that the ball was initially at rest with initial velocity
denote the velocity of the ball right before it hits the ground. Note that since the question states the ball was "dropped", assume that the ball was initially at rest with initial velocity
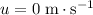 .
.
Under the assumptions, the acceleration
 of the ball will be constantly
of the ball will be constantly
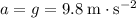 .
.
Rearrange the SUVAT equation
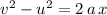 to find the final velocity
to find the final velocity
 of the ball right before landing:
of the ball right before landing:
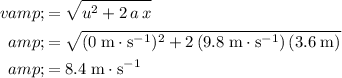 .
.