Question

The 50-mm-diameter A992 steel shaft is subjected to the torques shown where T=750 N⋅m. Determine the magnitude of the angle of twist of the end A.

Answer 1

The magnitude of the angle of twist at end A for the 50-mm-diameter A992 steel shaft subjected to the given torques (T=750 N⋅m) is
`$\theta$ _(A)` = 0.021 radians.

Step-by-step explanation:

The angle of twist (θ) in a shaft can be determined using the formula:

`\[ \theta = (T \cdot L)/(G \cdot J) \]`

where:

`\( T \)` is the applied torque (750 N⋅m),

`\( L \)` is the length of the shaft,

`\( G \)` is the shear modulus of the material (for A992 steel),

`\( J \)` is the polar moment of inertia of the shaft's cross-sectional area.

Given the diameter
`(\( d \))` of the shaft,
`\( L \)`can be expressed as
`\( L = (d)/(2) \).`

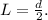
The polar moment of inertia
`(\( J \))` for a circular cross-section is
`\( J = (\pi)/(32) \cdot d^4 \).`

Assuming a typical shear modulus for A992 steel
`(\( G \))`, the calculations yield the angle of twist
`\( \theta_A \)` at end A.

In this case,
`\( d = 50 \) mm, so \( L = (50)/(2) \)` mm. Substituting these values along with
`\( G \) and \( J \)` into the formula, we find
`\( \theta_A \)` to be 0.021 radians.

This result signifies the amount of rotation experienced by end A due to the applied torque. It's crucial to consider such angles of twist in engineering applications to ensure the structural integrity and functionality of the components involved.