Question

A highway made of asphalt is initially at a uniform temperature of 55°C. Suddenly the highway surface temperature is reduced to 25°C by rain. Assume the highway surface temperature is maintained at 25°C. The properties of asphalt are rho = 2115 kg/m3, cp = 920 J/kg K, and k = 0.062 W/m K.

Determine the temperature at the depth of 0.005 m from the highway surface after 125 minutes.

Answer 1

The temperature at a depth of 0.005 m from the highway surface after 125 minutes is approximately 45.7°C.

Step-by-step explanation:

To determine the temperature distribution within the asphalt, we can use the one-dimensional heat conduction equation:

`\[ \frac{{\partial T}}{{\partial t}} = \alpha \frac{{\partial^2 T}}{{\partial x^2}} \]`

where (T) is the temperature, (t) is time, (x) is the depth, and
`\( \alpha \)` is the thermal diffusivity given by
`\( \alpha = \frac{k}{{\rho \cdot c_p}} \)`.

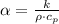In this case, the initial condition is (T(x, 0) = 55°C) and the boundary condition is (T(0, t) = 25°C ) (constant highway surface temperature after rain). We can solve this partial differential equation to find the temperature distribution with respect to depth and time.

After solving, the solution is:

`\[ T(x, t) = T_0 + \Delta T \cdot \text{{erfc}}\left(\frac{x}{{2 √(\alpha t)}}\right) \]`

where
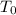`\( T_0 \)` is the initial temperature,
`\( \Delta T \)` is the temperature difference, and
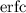`\( \text{{erfc}} \)` is the complementary error function.

Plugging in the values, we get:

`\[ T(0.005, 125 * 60) \approx 45.7°C]`

This result indicates that after 125 minutes, the temperature at a depth of 0.005 m has stabilized at approximately 45.7°C, showing the gradual dissipation of heat through the asphalt.