Question

Carbon dioxide enters an adiabatic nozzle at 1400 K with a velocity of 60 m/s and leaves at 600 K. Assuming constant specific heats at room temperature, determine the Mach number at the inletAssume that Carbon dioxide is an ideal gas under the state conditions.

Answer 1

The Mach numbers: At the Inlet (a):
`\[(T_2)/(T_1) = \left(1 + (\gamma - 1)/(2)M_{\text{inlet}}^2\right)\]` Solve for
`\(M_{\text{inlet}}\).`

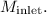
At the Exit (b):
`\[(T_2)/(T_1) = \left(1 + (\gamma - 1)/(2)M_{\text{exit}}^2\right)\]` Solve for
`\(M_{\text{exit}}\).`

Step-by-step explanation:

To find the Mach numbers at the inlet and exit of the adiabatic nozzle, we can use the isentropic relations for ideal gases. The isentropic relations relate the Mach number M , temperature T , and other properties across a nozzle or diffuser.

The isentropic relations for an ideal gas are as follows:

1. Isentropic relation for temperature and Mach number:

`\[(T_2)/(T_1) = \left(1 + (\gamma - 1)/(2)M^2\right)\]`

where:

-
`\(T_1\)` is the initial temperature (in Kelvin) at the inlet,

-
`\(T_2\)` is the final temperature (in Kelvin) at the exit,

-
`\(\gamma\)` is the ratio of specific heats
`(\(C_p/C_v\))`,

-
`\(M\)` is the Mach number.

2. Isentropic relation for velocity and Mach number:

`\[(V_2)/(V_1) = (1)/(M)\sqrt{(T_2)/(T_1)\left((\gamma + 1)/(2) + (\gamma - 1)/(2)M^2\right)}\]`

where:

-
`\(V_1\)`is the initial velocity at the inlet,

-
`\(V_2\)` is the final velocity at the exit.

Given:

-
`\(T_1 = 1400 \, \text{K}\)` (initial temperature at the inlet),

-
`\(T_2 = 600 \, \text{K}\)`(final temperature at the exit),

-
`\(V_1 = 60 \, \text{m/s}\)` (initial velocity at the inlet),

-
`\(\gamma = 1.289\)` (ratio of specific heats for carbon dioxide).

Now, let's calculate the Mach numbers:

At the Inlet (a):

`\[(T_2)/(T_1) = \left(1 + (\gamma - 1)/(2)M_{\text{inlet}}^2\right)\]`

Solve for
`\(M_{\text{inlet}}\).`

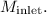
At the Exit (b):

`\[(T_2)/(T_1) = \left(1 + (\gamma - 1)/(2)M_{\text{exit}}^2\right)\]`

Solve for
`\(M_{\text{exit}}\).`

These equations are non-linear, and you may need to use numerical methods or specialized software to find the Mach numbers accurately. If you have access to engineering software or online calculators, they can provide a quick solution.