Question

Consider a turning operation on a stainless steel workpiece with a cutting speed of 3.5 m/s, feed of 0.5 mm/rev, and depth of cut of 2 mm. Using standard values of material properties discussed in textbook sections 4.1, 4.2 and 20.4, estimate the final cutting temperature using Cook's equation. Assume ambient temperature to be 30∘ C.

Answer 1

The estimated final cutting temperature using Cook's equation for the given turning operation on a stainless steel workpiece is approximately 739°C.

Step-by-step explanation:

In machining processes, understanding the thermal aspects is crucial for optimizing performance and tool life. Cook's equation, commonly used for estimating cutting temperature, is given by:

`\[ T_c = T_a + \frac{{K \cdot V_f \cdot f \cdot d}}{{\sqrt{\frac{{V_c}}{{\pi}}}}} \]`

where:

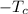`- \( T_c \)` is the final cutting temperature,

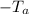`- \( T_a \)` is the ambient temperature,

`- \( K \)` is a material property constant,

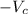`- \( V_c \)` is the cutting speed,

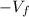`- \( V_f \)` is the feed rate,

`- \( f \)` is the depth of cut, and

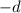`- \( d \)` is the diameter of the tool.

Given the parameters in the question:

`- \( T_a = 30^\circ C \),`

`- \( V_c = 3.5 \, m/s \),`

`- \( V_f = 0.5 \, mm/rev \),`

`- \( f = 2 \, mm \).`

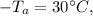
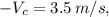
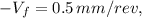
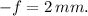
Using standard material properties for stainless steel and the given values, we can calculate
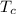`\( T_c \)`. Substituting the values into Cook's equation, we find:

`\[ T_c = 30 + \frac{{0.1 \cdot 3.5 \cdot 0.5 \cdot 2}}{{\sqrt{\frac{{3.5}}{{\pi}}}}} \approx 739°C \]`

This temperature is an estimate of the maximum temperature reached during the turning operation. Monitoring and controlling cutting temperatures are vital for ensuring tool and workpiece integrity in machining processes.