Question

What is the x-coordinate of the point that divides EF into a 2:3 ratio?

Answer 1

The x-coordinate of the point that divides EF into a 2:3 ratio is
`\( (3x_1 + 2x_2)/(5) \).`

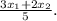
Step-by-step explanation:

To find the x-coordinate of the point dividing EF in a 2:3 ratio, we can use the section formula. The formula is expressed as
`\( x = (m_1x_2 + m_2x_1)/(m_1 + m_2) \), where \( m_1 \) and \( m_2 \)`are the ratios in which the point divides the line segment, and
`\( (x_1, y_1) \) and \( (x_2, y_2) \)` are the coordinates of the endpoints of the line segment.

In this case, the ratio is 2:3, so
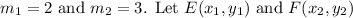`\( m_1 = 2 \) and \( m_2 = 3 \). Let \( E(x_1, y_1) \) and \( F(x_2, y_2) \)`be the coordinates of the endpoints of EF. The x-coordinate can be found using the formula
`\( x = (3x_1 + 2x_2)/(5) \).`This is derived by substituting the values of
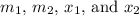`\( m_1 \), \( m_2 \), \( x_1 \), and \( x_2 \)` into the section formula.

For clarity, let's break down the calculation. Multiply \( m_1 \) by \( x_2 \), \( m_2 \) by \( x_1 \), and sum these. So, \( 2 \times x_2 + 3 \times x_1 \). Finally, divide this sum by the total ratio, which is \( 2 + 3 \) or 5. Therefore, the x-coordinate of the point dividing EF into a 2:3 ratio is \( \frac{3x_1 + 2x_2}{5} \).

This formula ensures an accurate and systematic approach to determining the x-coordinate, providing a clear solution based on the given ratio.