Question

Solve 100 points!!!!

Answer 1

1st option, y = 3x + 8

Explanation:

To find the equation of a line passing through two points, you can use the point-slope formula for a line, which is:

`y-y_1 =m(x-x_1)`

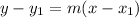
Where:

• '(x₁, y₁)' is a point on the line
• 'm' is the slope of the line

The slope 'm' can be calculated using the formula:

`m = (y_2-y_1)/(x_2-x_1)`

For the points given, (−1, 5) and (3, 17), we calculate the slope 'm' as follows:

`\Longrightarrow m = (17-5)/(3-(-1))=(12)/(4)=3`

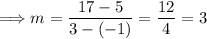
So the slope of the line is 3. Now, we use one of the points and the slope to write the equation of the line.

`\Longrightarrow y-5 =3(x-(-1))\\\\\\\\\Longrightarrow y-5 =3(x+1)`

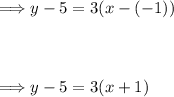
Now solve for 'y' to put the equation in slope-intercept form (y = mx + b):

`\Longrightarrow y-5 =3(x+1)\\\\\\\\\Longrightarrow y-5 =3x+3\\\\\\\\\therefore \boxed{y=3x+8}`

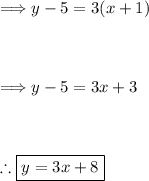
Thus, the first option is correct.

Answer 2

`\sf y = 3x + 8`

Explanation:

To find the equation of a line passing through two points
`\sf (x_1, y_1)` and
`\sf (x_2, y_2)`, we can use the point-slope form of the equation:

`\sf y - y_1 = m(x - x_1)`

where
`\sf m` is the slope of the line.

First, find the slope (
`\sf m`) using the given points
`\sf (-1, 5)` and
`\sf (3, 17)`:

`\sf m = (y_2 - y_1)/(x_2 - x_1)`

`\sf m = (17 - 5)/(3 - (-1))`

`\sf m = (12)/(4) = 3`

Now that we have the slope, let's use the point-slope form with one of the points, say
`\sf (-1, 5)`:

`\sf y - 5 = 3(x - (-1))`

Simplify the equation:

`\sf y - 5 = 3(x + 1)`

Distribute 3:

`\sf y - 5 = 3x + 3`

Add 5 to both sides:

`\sf y = 3x + 8`

So, the equation of the line passing through the points
`\sf (-1, 5)` and
`\sf (3, 17)` is:

`\sf y = 3x + 8`