Question

A measure of how well your linear model fits the dataset. reciprocal of the slope the y intercept correlation coefficient none of these is correct correlation of determination Question 2 I averaged the past 3 months of our shipments using the MAM method. However pointed out to me that we lost 2 days of work 2 months ago because of snow shu He suggested that I not treat all of the past 3 months data the same. What foreca should I now use? ESM You can't do what he wants to do with the data. Linear regression I averaged the past 3 months of our shipments using the MAM method. However, the boss pointed out to me that we lost 2 days of work 2 months ago because of snow shutdown days. He suggested that I not treat all of the past 3 months data the same. What forecast method should I now use? ESM You can't do what he wants to do with the data. Linear regression AESM WMAM Question 3 2 pts Given Y=3.5+4.77X when X=0 then Y=3.5. The term we use to describe this is point where the line crosses the Y axis is known as what? correlation coefficient none of these are correct. X,Y, and Z coordinates Given Y=3.5+4.77X when X=0 then Y=3.5. The term we use to describe this is point where the line crosses the Y axis is known as what? correlation coefficient none of these are correct. X,Y, and Z coordinates the Y intercept coefficient of determination Question 4 Analysts use this forecast method and manipulation of the data to try to get the prediction curve to match the actual curve more closely. They include coefficients involving both α and (1α) LPM AESM ESM Analysts use this forecast method and manipulation of the data to try to get the prediction curve to match the actual curve more closely. They include coefficients involving both α and (1α). LPM AESM ESM MAM WMAM Question 5 2pts As a rule of thumb, an analyst should never use more than 4 previous data points for any type of forecast method.

a.True
b.False

Answer 1

Question 1:

Final Answe:

The measure of how well your linear model fits the dataset is the coefficient of determination.

Step-by-step explanation:

The coefficient of determination, often denoted as R², is a statistical measure that represents the proportion of the variance in the dependent variable that is predictable from the independent variable(s). In the context of a linear model, the coefficient of determination indicates the goodness of fit of the regression line to the data points. It ranges from 0 to 1, where 1 indicates a perfect fit. The formula for R² is given by:

`\[ R² = 1 - \frac{SS_{\text{res}}}{SS_{\text{tot}}} \]`

where
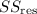`\( SS_{\text{res}} \)` is the sum of squared residuals (the differences between actual and predicted values), and
`\( SS_{\text{tot}} \)` is the total sum of squares.

Question 2:

Final Answer:

AESM (Additive Error Seasonal Model) is the recommended forecast method considering the variability in the past 3 months' data and the specific event of the snow shutdown days.

Step-by-step explanation:

In time series forecasting, especially when dealing with seasonality and unexpected events, an additive error seasonal model like AESM is appropriate. This model allows for adjustments to account for the variability introduced by the snow shutdown days, providing a more accurate representation of the underlying patterns in the data. Other methods like ESM (Exponential Smoothing Method) and WMAM (Weighted Moving Average Method) may not be as effective in capturing such nuances in the dataset.

Question 3:

Final Answer:

The term used to describe the point where the line crosses the Y axis is the Y intercept.

Step-by-step explanation:

In the given linear equation (Y = 3.5 + 4.77X), the coefficient 3.5 represents the Y intercept. This is the value of Y when X is equal to 0, indicating the point where the line intersects the Y axis on a Cartesian plane. The Y intercept is a key parameter in linear regression, providing information about the starting point of the regression line and its relationship with the dependent variable.

Question 4:

Final Answer:

Analysts use the Exponential Smoothing Method (ESM) for forecast manipulation, involving coefficients α and (1-α).

Step-by-step explanation:

ESM is a time series forecasting method that incorporates smoothing coefficients (α and 1-α) to manipulate data and closely align the prediction curve with the actual curve. The coefficients control the weights assigned to current and past observations, allowing analysts to adapt the model to capture trends and patterns in the data effectively. This flexibility makes ESM suitable for fine-tuning the forecast to match the actual data more closely.

Question 5:

Final Answer:

b. False

Step-by-step explanation:

The rule of thumb stating that an analyst should never use more than 4 previous data points for any forecast method is generally false. The appropriateness of the number of data points depends on the specific characteristics of the data and the forecasting method being employed. In some cases, more historical data may be necessary to capture trends and patterns accurately, and certain methods, such as time series models, often benefit from a larger dataset for improved accuracy. Therefore, the decision on the number of data points should be based on a careful analysis of the data and the requirements of the forecasting model.