Question

Find the step response of the following first-order control system using MATLAB. G(s)=44/(3s+1)

Answer 1

The step response of the given first-order control system G(s) =
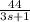`\((44)/(3s+1)\)` in MATLAB is
`\(y(t) = (44)/(3) \left(1 - e^{-(t)/(3)}\right)\).`

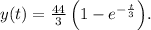
Step-by-step explanation:

In control systems engineering, the step response characterizes how a system behaves in response to a step input. For a first-order system, the transfer function G(s) is given as
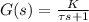`\(G(s) = (K)/(\tau s + 1)\)`, where K is the system gain and
`\(\tau\)` is the time constant. In our case,
`\(G(s) = (44)/(3s+1)\)`.

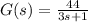To find the step response in MATLAB, we use the 'step' function, which simulates the system's response to a unit step input. In this case, the step response y(t) is given by
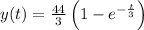`\(y(t) = (44)/(3) \left(1 - e^{-(t)/(3)}\right)\)`. This formula represents the system's output at any given time t after a step input. The term
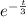`\(e^{-(t)/(3)}\)`accounts for the exponential decay component, and
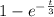`\(1 - e^{-(t)/(3)}\)` represents the rising part of the response.

It's crucial to understand that the time constant \(\tau\) influences the system's speed of response. In our case,
`\(\tau\)` is equal to 3, indicating that the system's output will reach approximately 63.2% of its final value within three time units. This analysis provides valuable insights into the dynamic behavior of the control system, aiding engineers in designing and optimizing systems for specific applications.