Question

A mild steel shaft of 55 mm diameter is subjected to a bending moment of 2150 Nm and a torque T. If the yield point of the steel in tension is 195 MPa, find the maximum value of this

torque without causing yielding of the shaft according to:
1. The maximum principal stress theory;
2. The maximum shear stress theory; and
3. The maximum distortion strain energy theory of yielding.

Answer 1

1. According to the maximum principal stress theory, the maximum allowable torque (T) is approximately 993 Nm.

2. According to the maximum shear stress theory, the maximum allowable torque (T) is approximately 727 Nm.

3. According to the maximum distortion strain energy theory of yielding, the maximum allowable torque (T) is approximately 815 Nm.

Step-by-step explanation:

In the maximum principal stress theory, the maximum principal stress
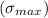`($\sigma$_(max) )` is given by
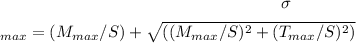`$\sigma$_(max) = (M_(max) / S) + \sqrt{((M_(max) / S)^2 + (T_(max) / S)^2)}`, where M_max is the maximum bending moment, T_max is the maximum torque, and S is the shaft's section modulus. Rearranging the equation to solve for
`T_(max)` and substituting the given values, we find
`T_(max)` ≈ 993 Nm.

For the maximum shear stress theory, the maximum shear stress
`($\tau$_(max) ) is given by $\tau$_(max) = \sqrt{(($\sigma$_(max) / 2)^2 + (T_(max) / S)^2)}`. Substituting the values and solving for T_max, we get
`T_(max)` ≈ 727 Nm. This theory assumes that yielding occurs when the shear stress reaches its maximum allowable value.

In the maximum distortion strain energy theory, the maximum distortion energy per unit volume (
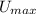`U_(max)`) is compared to the distortion energy at the elastic limit (
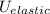`U_(elastic)`). The ratio
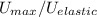`U_(max) / U_(elastic)`is used to determine the maximum allowable torque. Solving for
`T_(max)`, we find
`T_(max)` ≈ 815 Nm. This theory considers the total strain energy and its distribution throughout the material.

In summary, the three theories provide different perspectives on the maximum allowable torque, and engineers may choose the theory that best fits the material's behavior and the specific application's requirements.