The largest possible volume of the box is
 cm³ or 1265.625 cm³ (exact value, not decimal).
cm³ or 1265.625 cm³ (exact value, not decimal).
Let's denote the side length of the square base as x and the height of the box as h. Since the box has an open top, the volume (V) is given by the product of the base area and the height:
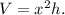
The total surface area of the box, including the open top, is the sum of the base area and the four vertical sides. The surface area (A) is given by:
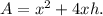
The available material to make the box is the surface area, which is given as 675 cm²:

To maximize the volume, we need to express h in terms of x . Solving the surface area equation for h :
![\[ h = (675 - x^2)/(4x) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wzhs4fzzqp9cjc940kc39u6rsrj3mfqbve.png)
Now, substitute this expression for h into the volume equation:
![\[ V = x^2 \left((675 - x^2)/(4x)\right) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4adx0lj2qpvb6zp6pw61mkztde3q6foba6.png)
Simplify the expression for V :
![\[ V = (675x - x^3)/(4) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/p1nudyx4c6lmernteuwk2e10zakxr20cix.png)
To find the maximum volume, take the derivative of V with respect to x and set it equal to zero:
![\[ 675 - 3x^2 = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bvxghxvnq6qwiltmhpgerngraf2qtzflnw.png)
Solving for x:
![\[ x^2 = (675)/(3) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zuwc7te8qxz0gc4xt5wddy832g7jkj73ht.png)
![\[ x^2 = 225 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qbst6vy5a6sln6s8o1fu1hx71p9ypmbkfi.png)
![\[ x = 15 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/68p2f1yca9m1jlalj074xjqfhyv3t9yjf0.png)
Now, substitute x = 15 back into the expression for h :
 =
=
![(225)/(4) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/gos0e09u5ckm78tokbnp1av2g9o1hhrxyx.png)
Now, find the volume V with x = 15 and
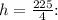
 =
=
 =
=
![(5062.5)/(4) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/d1bpeuy6esiwa4zqmat8siul6uahid81b9.png)
Therefore, the largest possible volume of the box is
 =
=
 cm³. The exact answer is
cm³. The exact answer is
 cm³.
cm³.