Final Answer:
The expected profit of three years of operations, where warehouse space is leased on the spot market, is $6,416,067.
Step-by-step explanation:
In order to calculate the expected profit, we need to construct a decision tree considering the different scenarios and their probabilities for each year. For the first year, the calculation is straightforward:
![\[ \text{Expected Profit Year 1} = (\text{Revenue} - \text{Cost of Warehouse Space}) * (1 + \text{Discount Rate})^(1) \]](https://img.qammunity.org/2024/formulas/business/college/3hh4w1hh3kx93g2rlt5h6qc1cjwpgu3vat.png)
For the second and third years, we need to consider the probabilistic nature of changes in demand, revenue, and warehouse space prices. The expected profit for each year can be expressed as:
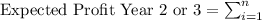

![* (1 + \text{Discount Rate})^(i) \right] \]](https://img.qammunity.org/2024/formulas/business/college/mba97rkcpmkf420642u8nr597qiamono3i.png)
Where
 is the probability of scenario ( i ), and ( i ) represents the possible outcomes.
is the probability of scenario ( i ), and ( i ) represents the possible outcomes.
By calculating the expected profits for each year and summing them up, we arrive at the total expected profit over the three-year period. This incorporates the uncertainties in demand, revenue, and warehouse space prices, providing a comprehensive estimate for Company XYZ's profitability under varying conditions. The discount rate ensures that future cash flows are appropriately adjusted to their present values.