Question

A 5.0kg kid comes down a slide from a height of 3.0 meters. At the bottom, he has a speed of 6.3m/s. The slide is 5.0 meters long. What is the frictional force acting on the kid?

A. 10N

B. 8.0N

C. 5.0N

D. 7.0N

E. 4.3N

Answer 1

The frictional force acting on the kid is approximately 9.555 N. None of the given options (A, B, C, D, E) match this value.

The frictional force acting on the kid can be determined using the concept of work and energy.

First, let's find the gravitational potential energy the kid has at the top of the slide. The formula for gravitational potential energy is:

Potential energy = mass * gravity * height

Given:

Mass (m) = 5.0 kg

Height (h) = 3.0 m

Gravity (g) = 9.8
`m/s^2`

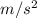
Potential energy = 5.0 kg * 9.8
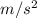`m/s^2` * 3.0 m

Potential energy = 147 J

Next, let's find the kinetic energy of the kid at the bottom of the slide. The formula for kinetic energy is:

Kinetic energy = 0.5 * mass *
`velocity^2`

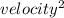
Given:

Mass (m) = 5.0 kg

Velocity (v) = 6.3 m/s

Kinetic energy = 0.5 * 5.0 kg *
`(6.3 m/s)^2`

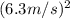
Kinetic energy = 99.225 J

Since energy is conserved, the potential energy at the top of the slide is equal to the kinetic energy at the bottom of the slide:

Potential energy = Kinetic energy

147 J = 99.225 J

To find the work done by friction, we can subtract the kinetic energy from the potential energy:

Work done by friction = Potential energy - Kinetic energy

Work done by friction = 147 J - 99.225 J

Work done by friction = 47.775 J

Finally, let's calculate the frictional force using the formula:

Work done by friction = force of friction * distance

Given:

Distance (d) = 5.0 m

47.775 J = force of friction * 5.0 m

Solving for the force of friction:

force of friction = 47.775 J / 5.0 m

force of friction ≈ 9.555 N

Therefore, the frictional force acting on the kid is approximately 9.555 N.

None of the given options (A, B, C, D, E) match this value