The angular displacement of each wheel is found using the kinematic equation for angular displacement. Calculating the initial angular velocity and substituting values yield the result for the given linear acceleration and time.
To find the angular displacement
 of each wheel during the acceleration period, we can use the kinematic equation relating linear acceleration
of each wheel during the acceleration period, we can use the kinematic equation relating linear acceleration
 , initial velocity
, initial velocity
 , time
, time
 , and angular displacement:
, and angular displacement:
![\[ \theta = \omega_0 t + (1)/(2) a t^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/o150a1v51r7syhp1cj80t48ddh4j61mt05.png)
where:
-
 is the initial angular velocity,
is the initial angular velocity,
-
 is the linear acceleration,
is the linear acceleration,
-
 is the time.
is the time.
First, calculate the initial angular velocity
 using the linear velocity and wheel radius:
using the linear velocity and wheel radius:
![\[ v_0 = \omega_0 r \]](https://img.qammunity.org/2024/formulas/physics/high-school/latyat7v2afkgx61d9q8sa3pa0ri1vdz5w.png)
![\[ \omega_0 = (v_0)/(r) \]](https://img.qammunity.org/2024/formulas/physics/high-school/7mkbii2b1nfh84uqmsj3p1nu2z9hnjgin8.png)
Given:
- Linear velocity,

- Wheel radius,
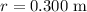
![\[ \omega_0 = \frac{20.0 \ \text{m/s}}{0.300 \ \text{m}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/k9u6pnvgdijsgbskynk3xi15o4koqo8xbz.png)
Now, substitute the known values into the angular displacement formula:
![\[ \theta = \left((v_0)/(r)\right)t + (1)/(2) a t^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/9m41npugn7czi7650j0apylnq80iumabxn.png)
Given:
- Linear acceleration,
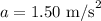
- Time,
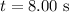
![\[ \theta = \left(\frac{20.0 \ \text{m/s}}{0.300 \ \text{m}}\right) \cdot 8.00 \ \text{s} + (1)/(2) \cdot 1.50 \ \text{m/s}^2 \cdot (8.00 \ \text{s})^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/jer5oks4r2h3jlo7499t8117cj4pns457k.png)
Calculate the angular displacement
 .
.