At the moment when the ladder's base is 30 ft from the building, it's slipping away from the building at a rate of
 feet per minute.
feet per minute.
Let's denote:
- \(x\) as the distance between the base of the ladder and the building.
- \(y\) as the height of the ladder on the building.
Given the ladder's length, \(y = 50\) ft, and it's sliding down the building at a rate of \(2\) ft per minute.
We're interested in finding the rate at which the base of the ladder (\(x\)) is slipping away from the building when \(x = 30\) ft.
Using the Pythagorean theorem for the relation between \(x\) and \(y\):
![\[x^2 + y^2 = 50^2\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/haf6s4hacvqfhggj43tp02krybfqix3ikw.png)
![\[y = √(50^2 - x^2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ijx2kljqgjibr8rck7tv7ksqv1q8k4nkeg.png)
Differentiating both sides of the equation with respect to time (t):
![\[(dy)/(dt) = (d)/(dt)\left(√(50^2 - x^2)\right)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2mg4r4h76fx9jenu1lsbunmik17t99rtf0.png)
Now, differentiate with the chain rule:
![\[(dy)/(dt) = (d)/(dx)\left(√(50^2 - x^2)\right) \cdot (dx)/(dt)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/at2bq0s5gm0zmhr0pv8x5vw1aa2xcu98zy.png)
When \(x = 30\):
![\[y = √(50^2 - 30^2) = 40\text{ ft}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4bnjbz012szb1r28p2ej39pp1k37jgdscj.png)
Differentiating
 :
:
![\[(dy)/(dt) = (-x)/(√(50^2 - x^2)) \cdot (dx)/(dt)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/kymk16nc9gnuwza0fi4f4xmczifhjz5z0k.png)
At
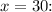
![\[(dy)/(dt) = (-30)/(40) \cdot 2 = -(3)/(4) \cdot 2 = -(3)/(2)\text{ ft/min}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/3pqdxq5zx0zfax3eyltdtmb9yh4c3ena0c.png)
Therefore, when the base is 30 ft from the building, it is slipping away from the building at a rate of
 ft/min.
ft/min.