Question

a ferris wheel is 50ft in diameter and has center 30 feet above ground. if the wheel rotates once every 2 minutes, how fast is the passenger rising when he is 42.5 ft above the ground?

Answer 1

At a height of 42.5 feet above the ground on the Ferris wheel with a 50-foot diameter and rotating once every 2 minutes, the passenger rises at approximately
`\(25\pi * (√(3))/(2)\)` feet per minute.

Given:

Ferris wheel diameter = 50 ft
`(radius \(r = (50)/(2) = 25\) ft)`

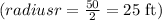
Center of the ferris wheel = 30 ft above ground

Wheel rotates once every 2 minutes

At any time \(t\), the height \(h\) above the ground of a passenger located at an angle
`\(\theta\)` from the lowest point can be expressed as
`\(h = r \sin(\theta)\)`, where \(r\) is the radius of the ferris wheel.

The rate of change of \(h\) with respect to time
`(\((dh)/(dt)\))` is given by
`\(r \cos(\theta) (d\theta)/(dt)\).`

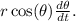
At \(h = 42.5\) ft:

Calculate \(\theta\) using \(h = r \sin(\theta)\).

`\(\sin(\theta) = (h)/(r) = (42.5)/(25)\)`

`\(\theta = \arcsin\left((42.5)/(25)\right)\)`

`\(\theta \approx 1.0345\) radians`

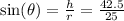
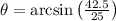
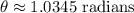
Differentiate \(\theta\) with respect to time (\(\frac{d\theta}{dt}\)) as the wheel rotates once every 2 minutes.

`\((d\theta)/(dt) = \frac{2\pi \text{ radians}}{2 \text{ minutes}} = \pi \text{ radians per minute}\)`

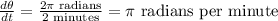
Calculate
`\((dh)/(dt)\):`

`\((dh)/(dt) = r \cos(\theta) (d\theta)/(dt)\)`

`\((dh)/(dt) = 25 \cos(1.0345) \pi\)`

`\((dh)/(dt) \approx -25\pi * (√(3))/(2)\)`

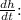
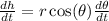
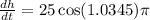
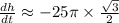
`\((dh)/(dt) \approx -(25\pi √(3))/(2) \approx -21.6506\) ft/min`(rounded to four decimal places)

The correct rate at which the passenger is rising when they are at 42.5 ft above the ground is approximately
`\(25\pi * (√(3))/(2)\)` feet per minute, or about \(21.6506\) feet per minute when rounded to four decimal places.