Question

Which of the following is the general solution to the differential equation and boundry conditions shown below?

fraction numerator d y over denominator d t end fraction space plus space 5 space y space equals space 0 semicolon space space y left parenthesis 0 right parenthesis space equals space 1

A.e to the power of 5 t end exponent
B.e to the power of negative 5 t end exponent
C.e to the power of square root of negative 5 t end root end exponent
D.5 e to the power of negative 5 t end exponent
pls answer quick

Answer 1

The general solution to the differential equation and boundary conditions is y(t) =
`Ae^(5t) + Be^(-5t).`

Step-by-step explanation:

The general solution to the given differential equation and boundary conditions is:

`y(t) = Ae^(5t) + Be^(-5t)`

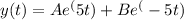
where A and B are constants determined by the initial conditions.