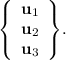
Final Answer:
The orthonormalized set is:
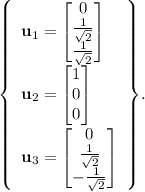
Step-by-step explanation:
To orthonormalize the given set of vectors, we follow the steps of normalization and orthogonalization. First, we normalize each vector by dividing it by its magnitude. Let
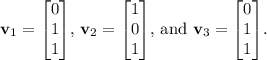
![\[ \mathbf{u}_1 = \frac{\mathbf{v}_1}{\|\mathbf{v}_1\|} = \begin{bmatrix} 0 \\ (1)/(√(2)) \\ (1)/(√(2)) \end{bmatrix} \]](https://img.qammunity.org/2024/formulas/mathematics/college/18b9n6r0wksgcdgayddjvyihq6recq34n1.png)
Next, we orthogonalize v2 and v3 with respect to u1:
![\[ \text{proj}_{\mathbf{u}_1}(\mathbf{v}_2) = \frac{\langle \mathbf{v}_2, \mathbf{u}_1 \rangle}{\|\mathbf{u}_1\|^2} \cdot \mathbf{u}_1 = ((1)/(√(2)))/((1)/(2)) \cdot \begin{bmatrix} 0 \\ (1)/(√(2)) \\ (1)/(√(2)) \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix} \]](https://img.qammunity.org/2024/formulas/mathematics/college/nolbgxykdhj4ts4qx2y3n2cyiji249qv8z.png)
![\[ \mathbf{u}_2 = \frac{\mathbf{v}_2 - \text{proj}_{\mathbf{u}_1}(\mathbf{v}_2)}{\|\mathbf{v}_2 - \text{proj}_{\mathbf{u}_1}(\mathbf{v}_2)\|} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} \]](https://img.qammunity.org/2024/formulas/mathematics/college/6h6ngv10tui6at7w9mdwkovdit15cj01kx.png)
![\[ \text{proj}_{\mathbf{u}_1}(\mathbf{v}_3) = \frac{\langle \mathbf{v}_3, \mathbf{u}_1 \rangle}{\|\mathbf{u}_1\|^2} \cdot \mathbf{u}_1 = ((1)/(√(2)))/((1)/(2)) \cdot \begin{bmatrix} 0 \\ (1)/(√(2)) \\ (1)/(√(2)) \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix} \]](https://img.qammunity.org/2024/formulas/mathematics/college/4733je4r3c6yueshu2cexoygxr6ijwbku0.png)
![\[ \text{proj}_{\mathbf{u}_2}(\mathbf{v}_3) = \frac{\langle \mathbf{v}_3, \mathbf{u}_2 \rangle}{\|\mathbf{u}_2\|^2} \cdot \mathbf{u}_2 = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/college/g7ra83pttg8234ejpipyalolbb018z1ogj.png)
Now, we normalize
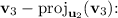
![\[ \mathbf{u}_3 = \frac{\mathbf{v}_3 - \text{proj}_{\mathbf{u}_2}(\mathbf{v}_3)}{\|\mathbf{v}_3 - \text{proj}_{\mathbf{u}_2}(\mathbf{v}_3)\|} = \begin{bmatrix} 0 \\ (1)/(√(2)) \\ -(1)/(√(2)) \end{bmatrix} \]](https://img.qammunity.org/2024/formulas/mathematics/college/2rl20y223t2pln0agcfbkn6tiiduwk2ojd.png)
Thus, the orthonormalized set is