Question

Write each fraction in terms of the LCD. [begin{array}{c} frac{x-6}{3 x²+4 x-4} ; frac{2}{x+2} frac{x-6}{3 x²+4 x-4}= frac{2}{x+2}=end{array}

Answer 1

To write each fraction in terms of the LCD, we can find the least common denominator (LCD) of the two fractions. In this case, the denominators are 3x²+4x-4 and x+2. The LCD is (x-2)(3x+2)(x+2). We can then rewrite the fractions using the common denominator.

Step-by-step explanation:

To write each fraction in terms of the LCD, we need to find the least common denominator (LCD) of the two fractions. The LCD is the smallest number that is divisible by all the denominators. In this case, the denominators are 3x²+4x-4 and x+2. To find the LCD, first factorize both denominators. The factors of 3x²+4x-4 are (x-2)(3x+2) and the factors of x+2 are (x+2). The common factors are (x-2)(3x+2)(x+2), which is the LCD. Now, we can rewrite the fractions using the common denominator: (x-6)/(3x²+4x-4) = ((x-6)*(x+2))/((x-2)(3x+2)(x+2)) and 2/(x+2) = (2*(x-2))/(x-2)(3x+2)(x+2)).

Answer 2

The given fractions,
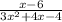`\( (x-6)/(3x^2+4x-4) \)` and
`\( (2)/(x+2) \)`, can be expressed in terms of the least common denominator (LCD) as follows:
`\( (2(x-6))/((x+2)(3x-2)) \)`.

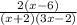Step-by-step explanation:

In order to write the fractions with a common denominator, we need to find their least common denominator (LCD). The LCD is the product of the distinct factors raised to their highest powers in all the denominators.

The denominators in the given fractions are
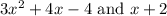`\(3x^2+4x-4\) and \(x+2\)`. Factoring
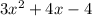`\(3x^2+4x-4\)`, we get
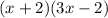`\( (x+2)(3x-2) \)`. Now, the LCD is (x+2)(3x-2).

Next, we rewrite each fraction with the common denominator. For the first fraction,
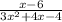`\( (x-6)/(3x^2+4x-4) \)`, we multiply the numerator and denominator by (2) to make the denominator (x+2)(3x-2). This results in
`\( (2(x-6))/((x+2)(3x-2)) \)`.

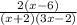Similarly, for the second fraction
`\( (2)/(x+2) \)`, we multiply the numerator and denominator by (3x-2) to obtain
`\( (2(3x-2))/((x+2)(3x-2)) \)`.

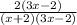Now, both fractions have the common denominator (x+2)(3x-2), and thus, the final expression is
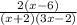`\( (2(x-6))/((x+2)(3x-2)) \)`. This is the simplified form of the given fractions in terms of the LCD.