Question

Use induction to prove that ( left(a }right){n}=a b{-n} a ) for all ( a, b \in G ) for ( n geq 0 ).

Answer 1

Final Answer:
`The statement \((a^n)^(-1) = a^(-n)\) for all \(a, b \in G\) and \(n \geq 0\) can be proven using mathematical induction.`

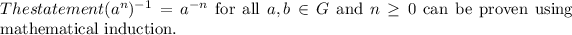
Step-by-step explanation:
`To prove this statement by induction, we start with the base case where \(n = 0\). In this case, \((a^0)^(-1) = a^(-0) = e\), where \(e\) is the identity element in the group \(G\). The base case holds true.`

`Next, assume that the statement holds for some arbitrary \(k \geq 0\), i.e., \((a^k)^(-1) = a^(-k)\). Now, we want to prove it for \(n = k + 1\).`

`Consider \((a^(k+1))^(-1)\). Using the assumption, we can express \(a^(k+1)\) as \(a \cdot a^k\). Therefore, \((a^(k+1))^(-1) = (a \cdot a^k)^(-1) = (a^k)^(-1) \cdot a^(-1)\). By the induction hypothesis, this is equal to \(a^(-k) \cdot a^(-1) = a^(-(k+1))\).`

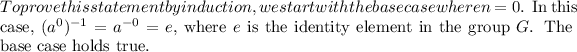
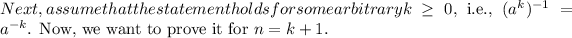
This completes the inductive step, and by the principle of mathematical induction, the statement
`\((a^n)^(-1) = a^(-n)\)` holds for all
`\(a, b \in G\)` and
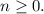`\(n \geq 0\).`Inductive proofs are powerful tools in mathematics, systematically establishing the validity of statements for an infinite set of values based on their truth for specific cases.